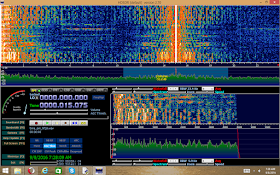
I wrote a new version of my AM modulator that does quadrature. When you use a plain cosine wave (f(x) = cos(x) rather than f(x)=cos(2*pi*freq)), it makes a carrier that is almost at 0. Suppressed-carrier mirrored audio is always present in the center of my quadrature output, and it corrupts the desired signal if you don't modulate it onto a higher frequency than 0, as pictured.

You may be asking, why cosine? Because I saw that the waveform of a sine is 90 degrees
ahead of a cosine, and unless I'm mistaken the Q should come 90 degrees
after the I. Using I=sin and Q=cos, it was backwards. Yesterday this drove me crazy until I realized and corrected the mistake in the script.
It makes the difference of which side of 0 the signals end up on. Here's a picture of how it should look:
Something I noticed is that if you increase the frequency value inside the script then the output sin/cos waves will look distorted in Audacity. However, the audio demodulated by HDSDR sounds great either way, so it's not distorting much.
Wave when f=2
Wave when f=12
I also found an interesting relationship between frequency (the f in sin(2*pi*f)), the file's sampling rate, and the resulting signal center frequency.
The original audio file was 48 kHz and so was the quadrature output since the script copies the headers. When f=12, the AM signal's center frequency was about 10.1 kHz. When I fed the script a copy of the audio that was upsampled 4x to 192 kHz, the center frequency became 40.2 kHz. Changing f from 12 to 2 while keeping the 192 kHz rate made a precisely 6.7 kHz signal. In the case of 192 kHz that means (center_frequency / f) = 3.35.
In the case of 48 kHz, the constant is different. I generated a file with f=2 and a rate of 48 kHz to see the constant. In this scenario, the carrier wasn't on an easily readable frequency boundary, so I set RBW to 0.2Hz and zoomed in fully. I estimated it to be 1.675 kHz.
Well, it turns out I was only 8 Hz off. Rearranging the formula above: if constant = (center_frequency / f), then
centerfrequency = constant * f
With 48 kHz, the constant is 0.841667, so the center frequency is 1.683 kHz.
And one more relationship to tie it all together: notice how the constant for 192 kHz is close to 4x the constant for 48 kHz. So close, in fact, that we can approximate this:
constant(sampling_rate) = ~0.0175 * sampling_rate
where sampling_rate is kHz, not Hz. However, note that this is an approximation for estimation purposes and is NOT as accurate as the f versus center frequency constants.
Finally, here's the Python script used to generate everything illustrated here. It makes separate I and Q mono WAV files which you must put together as left and right stereo channels, respectively.
------------------
import math
def radians(degrees):
return (degrees/360)*2*math.pi
#plt.axis([0,1000,0,255])
#plt.ylabel('some numbers')
samples=1000000
x=[]
i=[]
q=[]
multiplier=[]
demod=[]
amp=1
freq=2 #1/8
phase=0
for d in range(samples):
x.append(d)
#y.append(amp*math.sin((2*math.pi*freq*radians(d))+phase))
sinwavevalue=math.sin(radians(2*math.pi*freq*d))
coswavevalue=math.cos(radians(2*math.pi*freq*d))
i.append((coswavevalue/2)+0.5)
q.append((sinwavevalue/2)+0.5)
#multiplier.append(amp*math.sin((2*math.pi*freq*radians(d))+phase))
#for element in range(len(y)):
#demod.append(y[element]*multiplier[element])
#plt.plot(x,demod)
#plt.plot(x[0:1000],y[0:1000])
#plt.show()
bytepos=0
with open("D:/time8a.wav","rb") as infile: #Input File
with open("D:/time_am_f2_i.wav","wb") as o: #Output file
#byte = i.read(1)
for idx in range(0,44):
byte=infile.read(1)
o.write(byte)
while byte:
bytepos +=1
if (bytepos == samples):
break
test=float(float(int.from_bytes(byte,byteorder="big"))*i[bytepos])
#test=float(127*i[bytepos])
#print(int.from_bytes(byte,byteorder="big")," * ",y[bytepos]," = ",float(float(int.from_bytes(byte,byteorder="big"))*y[bytepos]))
tmp = [int(test),]
#print(bytes(tmp)," (",int(test),")")
o.write(bytes(tmp))
byte = infile.read(1)
bytepos=0
with open("D:/time8a.wav","rb") as infile: #Input File
with open("D:/time_am_f2_q.wav","wb") as o: #Output file
#byte = i.read(1)
for idx in range(0,44):
byte=infile.read(1)
o.write(byte)
while byte:
bytepos +=1
if (bytepos == samples):
break
test=float(float(int.from_bytes(byte,byteorder="big"))*q[bytepos])
#test=float(127*q[bytepos])
#print(int.from_bytes(byte,byteorder="big")," * ",y[bytepos]," = ",float(float(int.from_bytes(byte,byteorder="big"))*y[bytepos]))
tmp = [int(test),]
#print(bytes(tmp)," (",int(test),")")
o.write(bytes(tmp))
byte = infile.read(1)