VP9 ELI5 Part 6

Now it's time to create the actual image data. We're at the section labeled decode_tiles(sz - headerBytes), near the bottom. These functions are deeply nested, but by the end it will only be 4 levels so don't worry if it seems like each function leads to something else.

Here's what decode_tiles() looks like.

Now we need to define some state variables. Open Notepad++ and begin by adding the lines tileCols, tileRows, MiRowStart, MiRowEnd, MiColStart, and MiColEnd. Save it as state.txt.

There are a few more to add. Just add the name (ie MiCols) and the end value, not the formulas. For example, you should have "MiCols 120".

     MiCols = (FrameWidth + 7) >> 3 = 120
     MiRows = (FrameHeight + 7) >> 3 = 68
     Sb64Cols = (MiCols + 7) >> 3 = 15
     Sb64Rows = (MiRows + 7) >> 3 = 9

We'll need to keep this updated as we go along because some future functions depend on these values and it's easy to find them at the beginning.

Now let's fill in the values. We'll start with tileCols and tileRows. They depend on log2 functions. For our image, we opted (in the uncompressed header) to leave the log2 values at 0 because 2 ^ 0 = 1 and we only want 1 tile. So, tileCols = 1 << 0 (1 left-shift 0), which equals 1. tileRows works the same way so it will also equal 1. Therefore, we have 1 tile column and 1 tile row for a total of 1 tile. Fill in tileCols and tileRows in the text file.

Do you see the nested FOR loops, for (tileRow = 0... and for (tileCol = 0...? Since we only have 1 tileCol and 1 tileRow, these will execute only once. Therefore, we can pretend these loops don't exist and just perform everything once.

The first thing being done is the statement

     lastTile = (tileRow = tileRows - 1) AND (tileCol = tileCols - 1)
     = (0 = 0) AND (0 = 0)
     = (TRUE) AND (TRUE)

Both conditions are met, so lastTile will be TRUE. Now we look at the IF block, if (lastTile). Since lastTile is TRUE, all we have to do is tile_size = sz. But don't worry about that statement. We can't know it right now anyway.

Skipping the ELSE block, we have the MiRow/MiCol statements. Let's start evaluating these. tileRow and tileCol will be 0.

     MiRowStart = get_tile_offset( tileRow, MiRows, tile_rows_log2 )
     MiRowEnd = get_tile_offset( tileRow + 1, MiRows, tile_rows_log2 )
     MiColStart = get_tile_offset( tileCol, MiCols, tile_cols_log2 )
     MiColEnd = get_tile_offset( tileCol + 1, MiCols, tile_cols_log2 )

Here's what get_tile_offset() looks like.

     MiRowStart = 0
     MiRowEnd = 68
     MiColStart = 0
     MiColEnd = 120

Copy and paste these values into your text file. You'll need them later on.

The next statement is init_bool(tile_size), but since we're encoding we don't worry about that. That's for decoders to do. What we will do, however, is start our boolean encoder once we have some values to write.

Finally, the exciting part: decode_tile(). This is where our image data will go.

decode_tile()

To decode the single tile in the image, we have 2 nested FOR loops. The outer loop iterates through Rows, and the inner loop iterates through Columns. In X/Y terms, the row is Y and the column is X. So, you can see that the outer loop runs through Y while the inner loop runs through X. These FOR loops increment in steps of 8 because the Mi series of variables represents 8-pixel increments. Incrementing these by 8 equates to incrementing by 64, the size of a superblock.

Inside the nested loops, we have clear_left_context(). This just says that every time we finish a horizontal line and jump back to the left, we have to forget everything about the previous line's left side. Notice that it's only inside the outer loop.

In the inner loop, we iterate through superblocks (64x64 blocks). That's what decode_partition(r, c, BLOCK_64X64) does. Recall at the beginning how I said that VP9 images are broken into 64x64 superblocks. This is where that happens. Basically, this loop goes left-to-right from the top to the bottom, processing superblocks.

So for the first superblock, we'll be executing the statement decode_partition(0, 0, BLOCK_64X64).

These decoding functions are already nested pretty deep. Later I'll draw a diagram to show which functions we're running.

We can forget the first IF statement since it only applies to right or bottom edges of the image.

Add the following variables to your text file:

num8x8 = 8

halfBlock8x8 = 4

hasRows = true

hasCols = true

Now here's a hard part. partition is a Tree, a binary tree specifically. A video on these is shown below. We need to encode a value that says we want PARTITION_SPLIT so we can split the superblock into 4 32x32 blocks. We could say PARTITION_NONE and it would still yield 4 32x32 blocks, but then they would share a prediction mode (smudge function) and for better compression, we want each block to specify its own prediction mode. Using PARTITION_SPLIT lets us choose on a per-block basis.

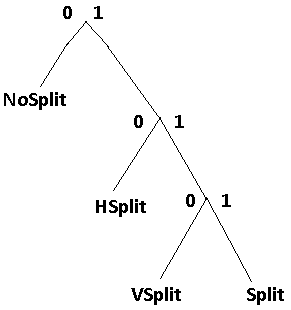
I had trouble with this part, but fortunately Ronald Bultje explained it to me and I drew a diagram of what he described. Here's my drawing of what the partition binary tree should look like.

We want Split, which breaks the block into 4 equal parts. In this case, that would break the 64x64 superblock into 4 32x32 blocks. That means we need to write 111 to the bitstream (using the bool-coder, of course).

(Advanced theory, not necessary to continue)

Credit: Ronald Bultje, in a chat with me on Nov 29, 2017

Here's the decoding side of this tree. I show it so we can work it backwards to encode.

The T[] array is the tree, which according to the spec is an array of integers. In this case it's partition_tree[] which may be found in the spec PDF.

Notice that read_bool() expects a probability, P(n >> 1). The >> is a logical shift of 1 bit, to the right. To find the probability to use when writing, we need to first run a complicated unnamed function (below).

To make a long story short, ctx will equal 15 at the end.

When the tree decoding function (9.3.3 Tree decoding process, above) first runs, n = 0. That means read_bool() will use P(0 >> 1) or just P(0) as the probability. Let's derive P(0).

hasRows = 1 (true) and hasCols = 1 (true). FrameIsIntra = 1 (true). This means we'll get our probability from partition_probs[ctx][node2]. We know that ctx is 15 and node2 = node = 0. So, we will retrieve the value partition_probs[15][0].

But there's a problem here. There's no such table as partition_probs in the VP9 spec PDF. How will we get the number we need? It turns out that we will use default_partition_probs[15][0], since we decided before that we would just use default probabilities.

default_partition_probs[15][0] = 10. So, our function will be read_bool(10). This means we need to write a 1 to the bitstream with a probability of 10. Let's keep a running tally of our bits and their probabilities, since we can't stop to write them now.

Running tally of bits

1, p = 10

Because we wrote a 1, read_bool() will return 1 when the video is decoded. Now refer to the binary tree shown above. Since we wrote a 1, we have a choice to write either 0 for a horizontal split (2 64x32's) or write another 1. We write another 1, and notice that we have to write just one more 1 to get Split.

Here are the passes the function will go through on the decode side:

1. n starts at 0. At the end, n = 2, which equals T[0 + read_bool(P(0 >> 1))] = T[1]
2. n starts at 2. At the end, n = 4, which equals T[2 + read_bool(P(2 >> 1))] = T[3]
3. n starts at 4. At the end, n = 5, which equals T[4 + read_bool(P(4 >> 1))] = T[5]

Since T[5] = -PARTITION_SPLIT (negative PARTITION_SPLIT) and the loop condition is that n is above 0, we exit the loop and return PARTITION_SPLIT without the negative sign. This means the decode_partition() function (section 6.4.3, shown near the beginning) now knows that we want the current superblock to be broken into 4 32x32 blocks. The partition variable in that function will equal PARTITION_SPLIT.

Before we start writing more bits, we need to know the probabilities to use. Notice that, during our tree loop, P(n >> 1) was changing. First it was P(0), then P(1), then P(2). We know that default_partition_probs[15][0] = 10, but what about default_partition_probs[15][1] and default_partition_probs[15][2]? Well, those are 7 and 6, respectively. The designers knew that the chance of a 0 diminishes as we go further down the tree, so they set the default probabilities accordingly.

Now that we have our probabilities, let's add the bits to our list.

Running tally of bits

1, p = 10

1, p = 7

1, p = 6

That was quite a lot. So where are we? Now that we know how to tell the video player that we want 4 32x32 blocks, we can go back to section 6.4.3, decode_partition().

Just under partition is subsize = subsize_lookup[ partition][ bsize ]. We know partition now, so we can plug it in. bsize is BLOCK_64X64. Basically, subsize_lookup lets us plug in a partition type along with our current block size and see how big the resulting block(s) would be. In our case, subsize will be 9 which corresponds to BLOCK_32X32.

Now we have a bunch of IF statements to go through. The first one checks if subsize is less than 8x8 or equal to 64x64. Neither of those is the case, so we move on to check if it's a horizontal split (64x32 in our case) and then we check if it's a vertical split (32x64 in our case). The ELSE block at the end of the IF statement reflects that if none of those conditions were met, which they weren't, then the only other possibility is a PARTITION_SPLIT.

Notice that inside the ELSE block, we have 4 decode_partition() statements. These are processed in raster order within the superblock. This means that superblocks are processed in raster order, and blocks within superblocks are processed the same way.

We're done here since we're calling decode_partition() again. When a function calls itself, as decode_partition() is doing right now, it's called recursion. In this case we have to recursively call ourselves to decode each of the 4 32x32's. Now would be a good time for a diagram of where we are.