Okay, so now that we've examined what RAW video data is composed of, we can get to work creating a valid VP9 video file.
For this step, we'll need to look at the VP9 bitstream specification PDF. Don't worry, I'll walk you through the whole thing. But first, read the section on video containers.
Video Containers
Once we have a valid VP9 frame we will need a
container to hold our finished VP9 video. A container is simply a file format that contains information for a video player like Media Player Classic to find individual frames in a file that would otherwise have been RAW.
Good container examples are *.MP4 and *.WAV files. MP4 isn't actually a video format, it's a file structure that can contain several different video formats, such as H.264. In a similar way, WAV isn't an audio format, it's simply a file that contains information about how to play RAW audio, usually LPCM.
We will be using an *.IVF (Indeo Video File) video container to hold our finished VP9 stream. It's really simply and easy to build in a hex editor.
Putting together a VP9 video
A standard VP9 bitstream is not a whole video as you might have assumed, but instead an individual frame. Think of a container (in our case, *.IVF file) as a ZIP archive with individual images. When encoding VP9, instead of compressing the entire video into one bitstream, we encode one frame, write it to the container file, and repeat until the end.
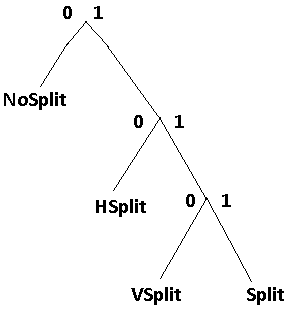
So a VP9 bitstream is just one frame. Here is how it is structured:
Adapted from the VP9 Bitstream Specification PDF.
We start with the uncompressed header (easy to generate), then write the compressed header, and finally start writing tile (image) data.
Advanced info: For simplicity and coding efficiency, we will only be dealing with 1 tile in our VP9 frames.
Here's the structure of a VP9 frame in text form. Don't worry that this doesn't make sense yet. We'll go bit-by-bit (literally).
Let's open Notepad++ and get started hand-crafting our bitstream.
We'll skip the first line startBitPos = get_position() and move on to uncompressed_header().
The bitstream spec defines different data structures depending on certain video parameters, so we need to define our parameters beforehand. We know it's a 960x540 image, but what Profile will the video be? VP9 supports 4 profiles, 0-3. Profile 0 is the default that YouTube videos are saved as. It can only carry 8-bit YUV 4:2:0. Profile 2 (the third profile) supports 10-bit pixels with YUV 4:2:0 color, so we'll be using Profile 2.
Here are the parameters we need to write, in order, in our case.
Uncompressed Header
frame_marker: 2 bits (1 0)
Always the case
profile_low_bit: 1 bit (0)
profile_high_bit: 1 bit (1)
Since Profile is 2 and 2 in binary is 10, the high bit is 1 and the low bit is 0.
show_existing_frame: 1 bit (0)
We are not trying to show a previously-decoded frame
frame_type: 1 bit (0)
0 means key frame, or initial image
show_frame: 1 bit (1)
Yes, we want to show the frame
error_resilient_mode: 1 bit (1)
Enable error resilient mode
Since frame_type = 0 (keyframe),
frame_sync_code: 24 bits (01001001 10000011 01000010)
color_config:
ten_or_twelve_bit: 1 bit (0)
0 because this is 10-bit data.
color_space: 3 bits (010)
Color space equals 2 (binary 010) for BT.709
color_range: 1 bit (0)
This designates Studio Swing, the 16-235 and 64-940 range limit we discussed earlier.
However, it is not enforced by the VP9 spec. It must be enforced by players.
frame_size:
frame_width_minus_1: 16 bits (0000001110111111)
959 in binary form
frame_height_minus_1: 16 bits (0000001000011011)
539 in binary form
render_size:
render_and_frame_size_different: 1 bit (0)
The render size will be the same as the frame size, 960x540
frame_context_idx: 2 bits (00)
Save our frame context into the 0 position
(not really important since we reset after each frame)
loop_filter_params:
loop_filter_level: 6 bits (000011)
Let's set this to 3 (11 binary)
loop_filter_sharpness: 3 bits (011)
Let's set this to 3 (11 binary)
loop_filter_delta_enabled: 1 bit (0)
Do not enable loop filter delta (being able to change the loop filter for
different parts of the image)
quantization_params:
base_q_idx: 8 bits (00000001)
Base quantizer (divisor for shrinking large values later on)
This provides the lossy part of VP9 compression. I've set it to 1 because
this is more about understanding the format and creating a valid image than
about compressing.
delta_coded: 1 bit (0)
No change to the quantizer required for the DC component of transforms of B/W image
(transforms are covered later)
delta_coded: 1 bit (0)
No change to the quantizer required for the DC component of transforms of
color add-on data
delta_coded: 1 bit (0)
No change to the quantizer required for the AC components of transforms of
color add-on data
segmentation_params:
segmentation_enabled: 1 bit (0)
Segmentation is a really cool feature but for simplicity we won't be using it.
tile_info:
increment_tile_cols_log2: 1 bit (0)
Do not increment that variable. Keep it at 0 since 2 ^ 0 = 1 and we only want 1 tile column.
tile_rows_log2: 1 bit (0)
Do not increment that variable. Keep it at 0 since 2 ^ 0 = 1 and we only want 1 tile row.
header_size_in_bytes: 16 bits (Can't know it yet; must complete next chapter first)
We'll pretend it's 16 0's (0000000000000000) for now.
Putting it together
So if you enter all these bits in order into Notepad++, you should start to have something like this:
(Obviously I superimposed this blog entry over Notepad++; I did not somehow manage to type formatted text in there)
Putting spaces between the fields is optional. I did it for clarity.
Anyway, once you've entered all the bits into Notepad++ (including the 16 0's for the end data we don't know), then you will need to press Ctrl+H to get the Find/Replace dialog if you added spaces. Skip this paragraph if you didn't add spaces. Clear the search field and press the spacebar once. Clear the Replace With field and press Replace All. Now there shouldn't be any spaces in the file.
Now that the spaces are gone, look at the status bar at the bottom of the window. If you entered the bits properly and removed any spaces, it should say Length: 112.
112 is divisible by 8 so this will fit in 14 bytes (112 / 8) without a need for extra empty bits to make a whole byte.
Now you'll need to separate the string of bits into groups of 8. Just start at the beginning, use your left arrow key to advance 8 characters, press Enter, and repeat. I know this is tedious, but don't worry, we only do this once.
It should look like this when it's done.
Now you can either manually copy-paste this one-by-one into MS Calculator in Bin mode and convert to Dec (tedious), or you can copy-paste the whole list into the top box at
https://www.textfixer.com/numbers/binary-to-decimal.php (recommended) and use that tool to get the whole list at once.
Now open a hex editor with decimal input support, such as HHD Hex Editor Neo. Create a new file, press Ctrl+1 (for Hex Editor Neo) to set it to decimal mode, click in the first blank entry in the large area on the left and start typing these numbers in order, pressing Enter after each one.
Save this file as "uncompressed_header". We will come back to it after we finish the next chapter.